Divide and Conquer
A general paradigm for parallel algorithms in which the master and slaves are doing the following:
| Master | Slaves |
loop while needed
divide the data among the slaves
compute something
retrieve and combine the results
from the slaves
process the final result
|
loop while needed receive data from the master compute something send the result to the master |
Data Exchange
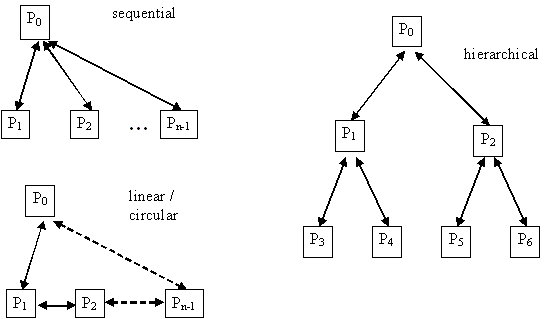
Communication Models

Linear communication
Each process sends the data to process number 0.
Master() // id == 0
{
for (i=1; i<no_proc; i++) {
Collect(recv_data, i);
Process_data(recv_data, my_data);
}
Process_final_result(my_data);
}
Slave()
{
Report(my_data, 0);
}
Optimization: in which the process 0 collects the data in any order. This way the other processes report the data in the order in which they finish their job.
Master() // id == 0
{
for (i=1; i<no_proc; i++) {
Collect_any(recv_data);
Process_data(recv_data, my_data);
}
Process_final_result(my_data);
}
Slave()
{
Report(my_data, 0);
}
Examples:
Computing an integral.
Divide_receive_data()
{
if (id == 0) {
input a, b;
Global_to_local(a, b);
{
}
Computation() // Function Compute_partial_integral
{
my_intg = 0;
low = id / no_proc;
dx = 1.0 / (n * no_proc);
for (i=0; i<n; i++)
my_intg += (F(low+(i+1)*dx) - F(low+i*dx)) / dx;
}
Process_data(recv_intg, my_intg)
{
my_intg += recv_intg;
}
Process_final_result(my_intg)
{
output "The integral is equal to ", my_intg;
}
Computing the Sum
In a shared memory model. Using no_threads for the number of
threads and id for the thread id, going from 0
to no_threads-1.
void *Thread(void *arg) {
int id = Get_id(), n, step, sum=0;
Global_to_local(n);
step = n/no_threads; // no_threads is global
for (int i=id*step; i<(id+1)*step; i++)
sum += a[i];
Report(sum, id);
}
// Linear Report Data
void Report(int sum, int id) {
lock(&data_mutex);
global_sum += sum;
threads_done++;
unlock(&data_mutex);
}
The data does not need to be collected in order. The master can check when the number of threads that are done is equal to no_threads to report the result.
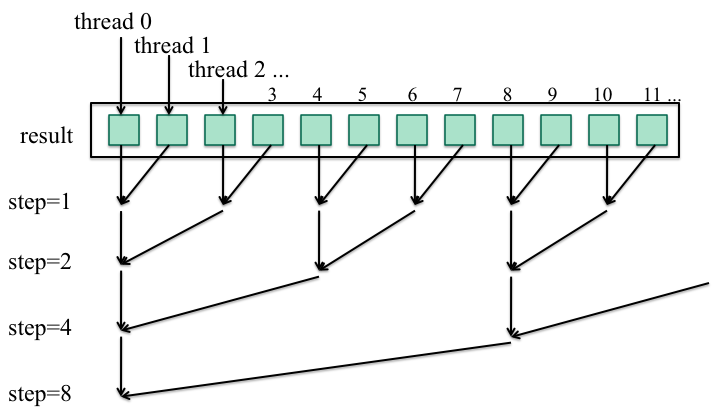
// Hierarchical Report
void Report(int sum, int id) {
result[id] = sum; // the result array is global
int step = 1;
while (2*step <= no_threads) {
Barrier(no_threads);
if (id % (2*step) == 0) {
result[id] += result[id+step];
}
step *= 2;
}
if (id == 0)
cout << result[0];
}
Finding if a number is prime
bool Is_prime(int n)
{
for (int i=2; i<= sqrt(n); i++)
if (n%i == 0)
return false;
return true;
}
Divide the interval [2, sqrt(n)] into no_threads intervals.
Parallel Prime Number
d = ceil((sqrt(n)-2)/no_threads);
Computation()
{
my_res = true;
for (i=id*d+2; i<(id+1)*d+2 && i<= sqrt(n) && my_res; i++)
if (n%i == 0)
my_res = false;
}
Report_data(my_res)
{
lock(&mutex);
if (!my_res)
global_res= false;
unlock(&mutex);
}
Master_prime() // for id = 0
{
input n; // global
d = ceil((sqrt(n)-2)/no_threads); // global
global_res = true;
Barrier(no_threads);
int my_res=true; // local
for (i=2; i<=d+1 && my_res; i++)
if (n%i == 0)
my_res = false;
Report_data(my_res);
Barrier(no_threads);
output global_res;
}
Slave_prime(id) {
Barrier(no_threads);
int my_res=true; // locals
int lim = min((id+1)*d+1, sqrt(n));
for (i=id*d+2; i<=lim && my_res; i++)
if (n%i == 0)
my_res = false;
Report_data(my_res);
Barrier(no_threads);
}
Computing with Interruption
Determining If a Number Is Prime
Global_to_local_res(int & my_res)
{
lock(&mutex);
if (!global_res)
my_res = false;
unlock(&mutex);
}
Master_prime() // for id = 0
{
input n; // global
d = ceil((sqrt(n)-2)/no_threads);
global_res = true;
Barrier(no_threads);
int my_res=true; // local
for (i=2; i<=d+1 && my_res; i++) {
Global_to_local_res(my_res);
if (n%i == 0)
my_res = false;
}
Report_data(my_res);
Barrier(no_threads);
output my_res;
}
Slave_prime(id)
{
Barrier(no_threads);
int my_res=true; // locals
int lim = min((id+1)*d+1, sqrt(n));
for (i=id*d+2; i<=lim && my_res; i++) {
Global_to_local_res(my_res);
if (n%i == 0)
my_res = false;
}
Report_data(my_res);
Barrier(no_threads);
}