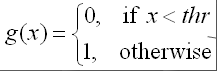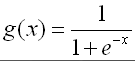Neural Networks

Neural Networks

• A learning model inspired by the structure of the brain.
• It's a parallel network of connected neurons taking in a number of parameters as input and returning a decision based on them as output.
• The connections are moderated by a set of weights, which is the part that the NN can learn.
• They have an extensive range of applications.
• The difficulty of the NN is considered to be the initial decision on their structure.

History of NN

• First neuron model by W. McCulloch and W. Pitts in 1943.
• Rosenblatt (1958) developed the idea of perceptron, a 3-layered NN.
• ADALINE (ADAptive LInear Element), an analogue electronic device built in 1960 by Widrow and Hoff (of Stanford University).
• 1969 Minsky and Papert wrote a book on the limitations of NN. This caused much funding to such research to be cut.
• The NNs re-emerged in the 70s and they seem to be a large success at the moment.

Why Use NN?

• Adaptive learning: they are capable to learn from the training data.
• Flexibility: they can be adapted quite easily to a range of problems with little domain-specific requirements.
• Self-organization: they are sometimes capable of learning not only the parameters, but also the representation or organization from the training set.
• Fault tolerance: by including redundant information coding they can adjust to partial destruction of the network.

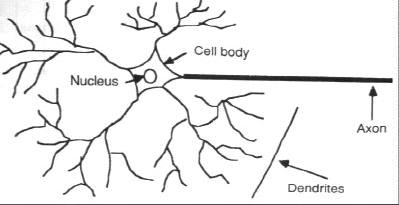
Neuron

• Biologically, a neuron is a brain cell. It is connected to other neurons and it operates by exchange of electrical signals.
• The processes taking place in the brain are considered to result from networks of neurons.
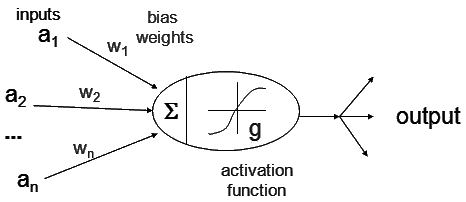
• The artificial neurons are units with a number of inputs and one output. Each of the inputs a_i has an associated bias weight w_i and the output is the result of as activation function g of the weighted sum of the inputs.
• output = g (Sum_i a_i w_i)

Neuron
 

Activation Function

• The most common functions are the simple threshold and the sigmoid.
• Threshold:
  
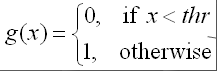
• Sigmoid:
  
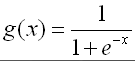
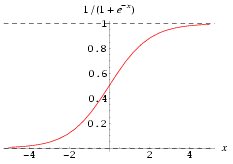
• The neuron can also work as a logic gate if the function is an And, Or, Not.
• And: weights = 1, thr = 2; Or: thr = 1. Not: weight = -1, thr=0.

Network Structure

• A NN is a directed graph of neurons. The output from one neuron can become the input for one or several other neurons.
• Feed-forward network: if the graph is acyclic.
• Recurrent network: when there are cycles in the graph so that the output of a neuron can come back as input after some processing.
• Input units: those whose inputs are external.
• Output unit(s): the output represents the answer a the entire NN.
• Hidden units: all the others.

Network Structure

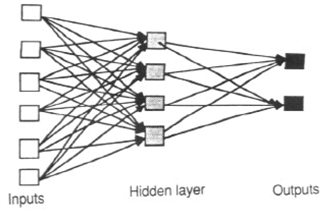
A feed-forward network
Layers: units at the same distance from the inputs.


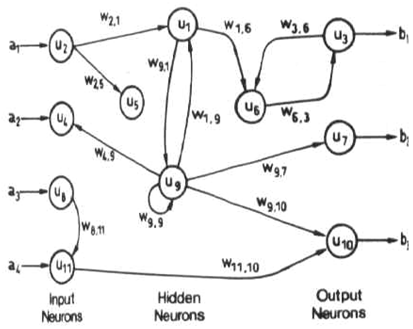
A recurrent network.

Example

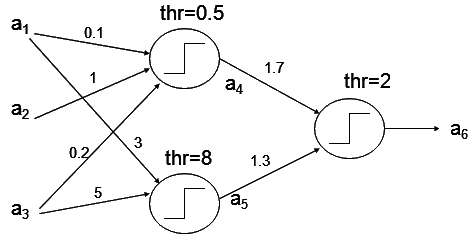
Given: a₁=2, a₂=0.05, a₃=3.
First sum: 0.1*2+0.05*1+0.2*3 = 0.85 => a₄=1
Second: 3*2 + 5*3 = 21 =>a₅ = 1
Third sum: 1.7*1 + 1.3*1 = 3 =>a₆ = 1 (output)

Perceptrons

• A perceptron is a single-layer feed-forward network.
• Their name comes from Frank Rosenblatt and they were popular in the 60s.
• Their goal is to extract some features from the input.
• They mimic the vision system of some animals.
• If the activation function is a threshold, the perceptron is a linear separator. In 2D it's a line, in 3D a plane, etc.

Delta Learning for a Neuron

• Suppose that we have some examples of input sets (x=<x₁, x₂, ..., x_n>) with known output (y).
• Error: the difference between the neuron's output and the desired output. Let h be the output of the neuron. We denote by
• Err = (y-h(x))
• Then we try to minimize the function
• E = 1/2 (y – h(x))2 = 1/2 (y-g(Sum_iw_ix_i))2.
• Computing the gradient of this and following the direction in which it decreases, we obtain
• w_i = w_i+a*Err*g'(x)*x_i,
• where a is the learning rate.

Back-Propagation Algorithm

• Suppose we have a feed-forward multi-layer network. The learning takes place in several epochs.
• An epoch consists in the following:
• Forward pass: compute the outputs from each neuron starting from the input layer going forward.
• Backward pass: starting from the output layer, apply the delta learning going backward. The error is propagated from the output layer to the last hidden layer and the delta learning can be applied, and so on.
• It can be proved that the network converges towards correct output for the given input after a number of epochs.

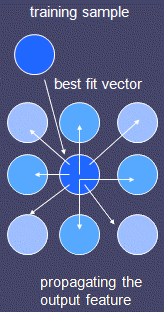
Self-Organizing Maps (SOM)

• SOMs are a data visualization technique invented by T. Kohonen in 1981 which reduce the dimensions of data through the use of self-organizing neural networks.
• The NN is organized in a grid structure where cells close to each other are supposed to have similar properties.
• For each training example, first we locate the closest cell based on the input values. Then we change the output of this cell to mach the result. Then we propagate the change to the adjacent cells.

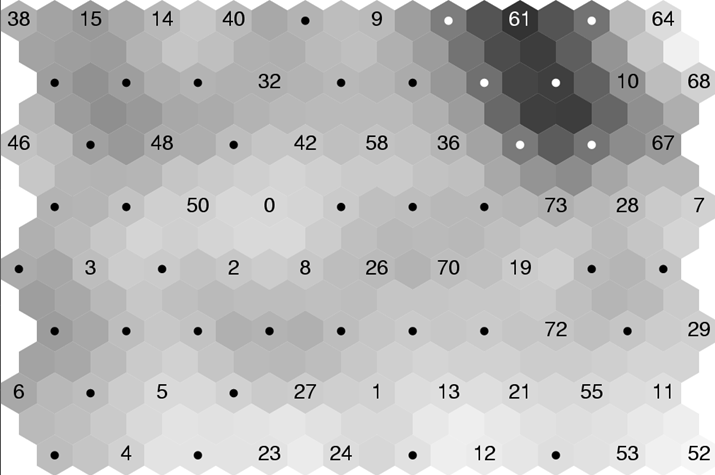
SOM
  

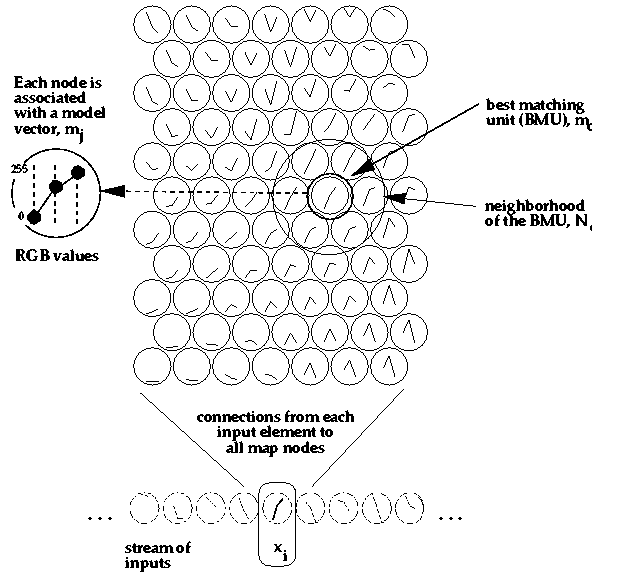
Example of trained SOM

Applications

• Problems for which there is no known solution or the solution involves a lot of parameters.
• Pattern recognition, image analysis: facial, fingerprint, textures, handwriting, speech.
• Sensors: electronic noses, analysis of medical images, lipreading.
• Data mining: identifying disease, forecasting.
• Business: assigning airplane seats, scheduling, credit evaluation.
• Autonomous systems, walking, swimming.
• http://tralvex.com/pub/nap/