Dana Vrajitoru
C311 Programming Languages
Regular Grammars, Scanners, DFA
DFA versus NFA
- DFA - deterministic finite state automaton.
- A state transition machine where from each state we can move to
one of the others based on the current terminal symbol.
- There at most one outgoing branch for each possible symbol.
- NFA - non-deterministic finite state automaton.
- The difference with a DFA is that there can be more than one
outgoing branch with the same symbol.
- Regular grammars can be translated as NFAs.
NFA to DFA
- To write a scanner more easily, we can transform an NFA into a
DFA.
- For this we construct a DFA where the states are combinations of
states from the NFA that represent alternatives that can be reached
from any given state with the same symbol.
- For example in the first grammar we would add a state called TV:
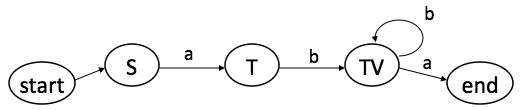
Example: NFA (top) and equivalent DFA (bottom)
Regular Expressions
- Recognized by regular grammars.
- They can be parsed by a linear algorithm that doesn't need to
store the global structure of the parsing tree.
- Only one non-terminal symbol is active at any moment.
- This type of parsing algorithm is called a scanner.
- The first compilation step, the lexical analysis, is done by a
scanner.
Examples
Finite States Machines
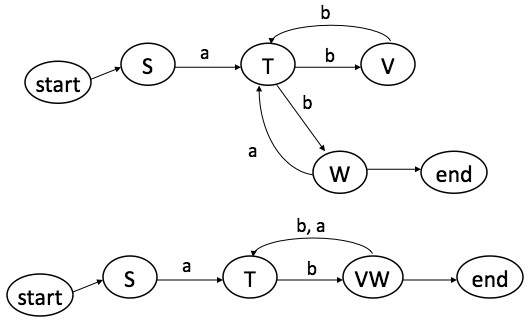
- A string (simple character means one that is not a quote, simple
quote, backslash):
S => " T
T => simple-character T
T => \ V
V => {"|'|\|n|t...} T
T => "
- Real Number
N => {-|+|e} UN
UN => UI . UI
UI => digit UI
UI => digit
- The second rule above is not a regular rule. It needs a parser and
not a scanner to be processed.
- We can transform it the following way:
UN => digit UN
UN => digit
UN => . UF
UF => digit UF
UF => digit
Scanner / Parser
- The lexical analysis of a program is done by a scanner.
- A scanner is based on a regular grammar where the end of any chain
of rules (a non-terminal converted to a single terminal) produces a
token as a result.
- The parsing process calls the scanner during its execution to
retrieve every new token, then processes it before invoking the
scanner again.
- They are not two separate phases: the scanner is called repeatedly
from the parser.
Scanner in Context
A scanner that works in the context of a program in which it
recognizes individual units.
It can be written to recognize the termination of a unit by a
character that is not part of it.
We can replace:
UN => digit UN
UN => digit
with:
UN => digit UN
UN => e
Table Driven Scanner
If the grammar is equivalent to a DFA, then we can organize the
rules in a table:
I => letter J
I => _ J
J => letter J
J => digit J
J => _ J
J => - J
J => e
Table:
| | letter | digit | _ | - | else
|
| I | J | err | J | err | err
|
| J | J | J | J | J | end
|


