Embarrassingly Parallel Algorithms

• Sometimes called naturally parallel algorithms.
• Simplest type of parallel algorithms requiring almost no communication between the processes.
• Each process can perform their own computations without any need for communication with the others.
• It may require some initial partition of the data or collecting the results in the end, but not always.

Ideal Case

• All the sub-problems or tasks are defined before the computations begin.
• All the sub-solutions are stored in independent memory locations (variables, array elements).
• Thus, the computation of the sub-solutions is completely independent.
• If the computations require some initial or final communication, then we call it nearly embarrassingly parallel.

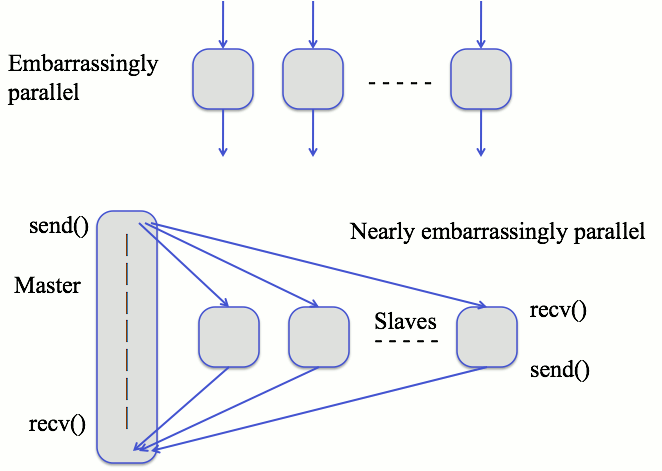
Variations / Hybrid Systems

• The solutions must be accumulated in a shared data structure - this requires some coordination at the end.
• Some non-obvious termination condition, such as something being found. This requires intermediate coordination.
• Not all sub-problems are known initially. Additional overhead necessary to keep track of the tasks (pool of tasks).

Classic Examples

• Protein folding software that can run on any computer with each machine doing a small piece of the work.
• SETI project (Search for Extra-Terrestrial Intelligence)
  SETI
• Generation of All Subsets.
• Generation of Pseudo-random numbers.
• Monte Carlo Simulations.
• Mandelbrot Sets (a.k.a. Fractals)

Monte Carlo Simulations

• Algorithms that approximate a function using random selections in calculations.
• Example: approximating pi by comparing the area of a circle to that of a rectangle enclosing it.
• If r is the radius of the circle, then the area of the rectangle is 4 r². That of the circle is pi r². The ratio between then is pi/4.
• A MC algorithm can generate n random points inside the rectangle, count the ones inside the circle, divide by the total, and multiply by 4.

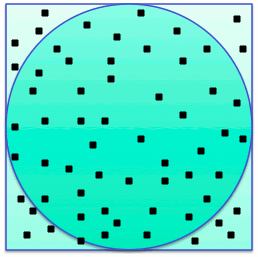
Total points: 65 Points inside the circle: 56 pi ~= 4*56/65 = 3.44615

Sequential Algorithm

Count_pt(int N) {
  double count_in = 0;
  for (i=0; i < N; i++) {
    x = randr(-1, 1);
    y = randr(-1, 1);
    if (x*x+y*y <= 1)
      count_in++;
  }
  return count_in;
}
Pi(N) {
  return 4*Count_pt(N)/N;
}

Parallel Algorithm

n = N/no_proc; // assuming N is a multiple of no_proc
Master_count(n) {   
  Broadcast(n, 0);
  my_count = Count_pt(n);
  for (i=1; i < no_proc; i++) {
    Recv(count, i);
    my_count += count;
  }
  return my_count;
}
Slave_count() {
  Broadcast(n, 0);
  my_count = Count_pt(n);
  Send(my_count, 0);
}

Pseudo Random Numbers

• Technique 1. One process can generate the pseudo-random numbers and send to other processes that need the random numbers. This is sequential.
• Technique 2. Use a separate pseudo-random number generator on each process. Each process must use a different seed. This is embarrassingly parallel.
• The choice of seeds used at each process is important. Simply using the process id or time of the day can yield to bad distributions. One can use the /dev/random device driver in Linux to get good seeds.
• Technique 3. Convert the linear generator such that each process only produces its share of random numbers. It is easier to control but requires more communication.

An Example
A common way to generate pseudo-random numbers is using large primes a and c:
y0 = s; // the seed
y₀ = s;
y_i+1 = a y_i + c
We can convert it to a dependency on a number several positions back.
y_i+k = a^k y_i + (a^k-1 + ... + a² + a + 1) c = a^k + c (a^k-1)/(a-1)

k Steps If we denote by A = a^k and C = c(a^k-1)/(a-1), then
y_i+k = A y_i + C (*)
computes the k^th next number in the sequence.

The master computes p₀, p₁, ..., p_k-1 using the simple formula, then sends them to each process.

Each process generates its own random numbers from the seed received from the master using (*).